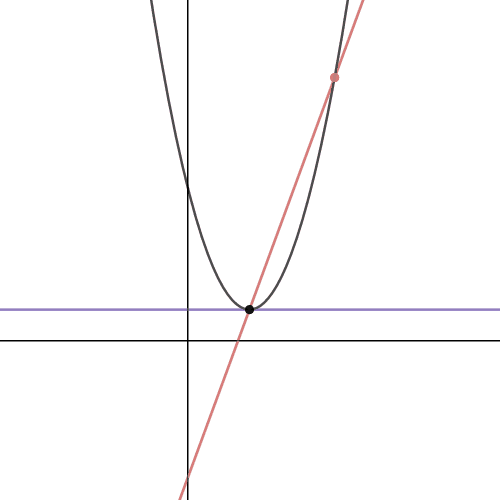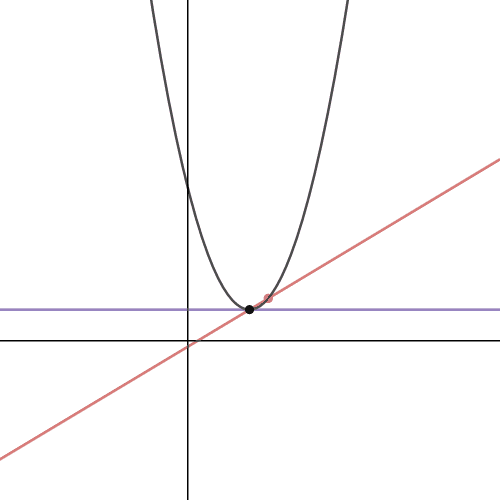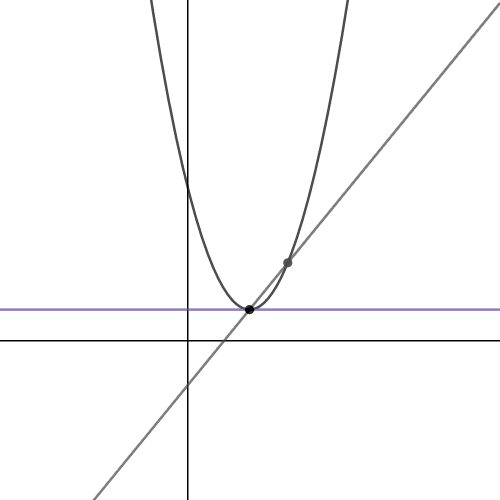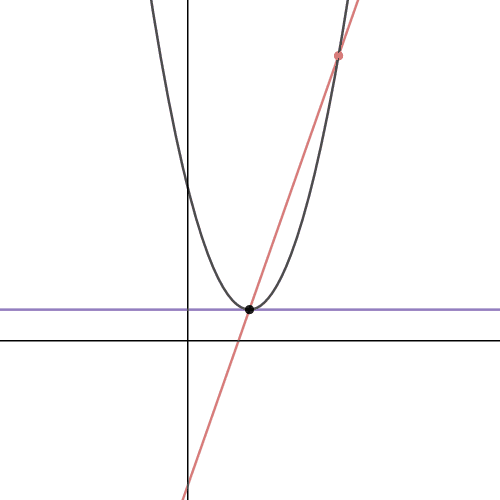
| Webmatematik: Monotoniforhold Matlet: Monotoniforhold FriViden (Video 8-11): Monotoniforhold Wikipedia: Monotoni (matematik) |
søndag den 31. maj 2015
Funktionsanalyse 3
Cirklens omkreds 1
| Vinkelsum i polygon (n-kant): S = ∑n − 2i = 1180 Sidelængde i n-kant: s = √r2 + r2 − 2 ⋅ r2 ⋅ cos( 2πn ) s2 = r ⋅ sin( 2 ⋅ πn )sin( π2 − πn ) |
lørdag den 30. maj 2015
Cirklens omkreds 0
| Vinkelsum i polygon (n-kant): S = ∑n − 2i = 1180 Sidelængde i n-kant: s = R ⋅ ( tan( πn − π ) − tan( − πn ) ) Wikipedia: Cirkel |
Funktionsanalyse 2
| Webmatematik: Monotoniforhold Matlet: Monotoniforhold FriViden (Video 8-11): Monotoniforhold Wikipedia: Monotoni (matematik) |
torsdag den 28. maj 2015
Funktionsanalyse 1
| Webmatematik: Monotoniforhold Matlet: Monotoniforhold FriViden (Video 8-11): Monotoniforhold Wikipedia: Monotoni (matematik) |
onsdag den 27. maj 2015
Integral Calculator (Riemann)
| YouTube Video: Approximating Integrals with Desmos For dummies: Riemann Sum Formula for the definate Integral Wikipedia: Integralregning Wikipedia: Bernhard Riemann |
tirsdag den 26. maj 2015
mandag den 25. maj 2015
Førstegradspolynomium (1)
| f ( x ) = x2 g ( x ) = ddxf ( x ) = 2x y − f ( x0 )x − x0 = g ( x0 ) y − f ( x0 ) = g ( x0 ) ( x − x0 ) y = g ( x0 ) ( x − x0 ) + f ( x0 ) |
Førstegradspolynomium (0)
Approksimerende førstegradspolynomium
y = 0.5 x3 - 3 x + 1
y = 0.5 x3 - 3 x + 1
|
| Approksimerende førstegradspolynomium f ( x ) = x2 g ( x ) = ddxf ( x ) = 2x y − f ( x0 )x − x0 = g ( x0 ) y − f (x0 ) = g ( x0 ) ( x − x0 ) y = g ( x0 ) ( x − x0 ) + f ( x0 ) |
Førstegradspolynomium (0)
| Approksimerende førstegradspolynomium f ( x ) = x2 g( x ) = ddxf ( x ) = 2x y − f ( x0 )x − x0 = g ( x0 ) y − f ( x0 ) = g ( x0 ) ( x − x0 ) y = g ( x0 ) ( x − x0 ) + f ( x0 ) |
søndag den 24. maj 2015
Sammensat funktion (differentiation)
| f ( g ( x ) ) → f ' ( g ( x ) ) ⋅ g ' ( x ). f ( x ) = 14 ⋅ √x g ( x ) = 5 ⋅ x3 f ' ( g ( x ) ) ⋅ g ' ( x ) = ( 5 ⋅ x3 )−0,5 ⋅ 15 ⋅ x28 |
lørdag den 23. maj 2015
Kvadratrod x (differentialregning)
| f ( x ) = √ x = x0,5 ddx f ( x ) = 12 ⋅ x−0,5 = x−0,52 = x−0,52 ⋅ x0,5x0,5 = x−0,5 + 0,52 ⋅ x0,5 = 12 ⋅ √ x |
fredag den 22. maj 2015
torsdag den 21. maj 2015
Differenskvotient (sekanthældning)
|
Tangenthældningen (differentialkvotienten i x₀) er grænseværdien af differenskvotienten for h gående mod 0: at = limh → 0( as ) = limh → 0( h + ½ x0 ) = ½ x0 Web-matematik |
tirsdag den 19. maj 2015
søndag den 17. maj 2015
Abonner på:
Kommentarer (Atom)