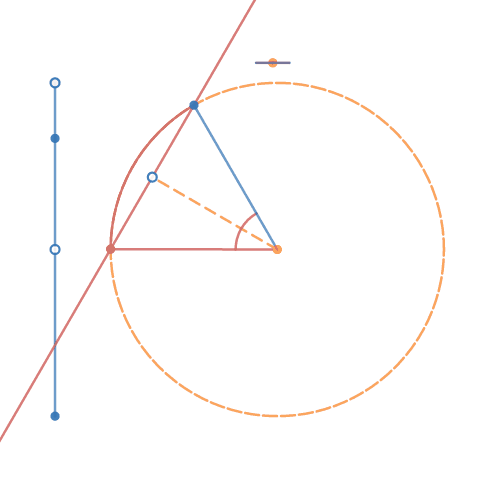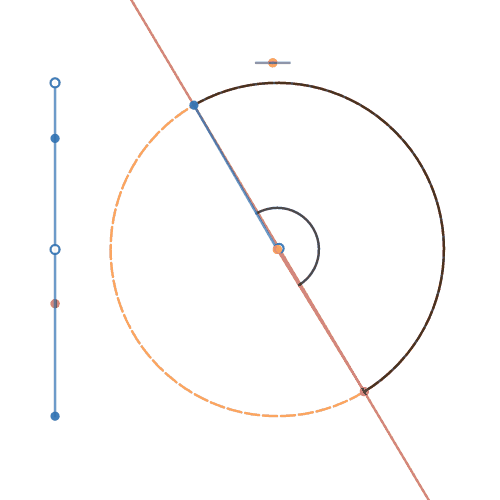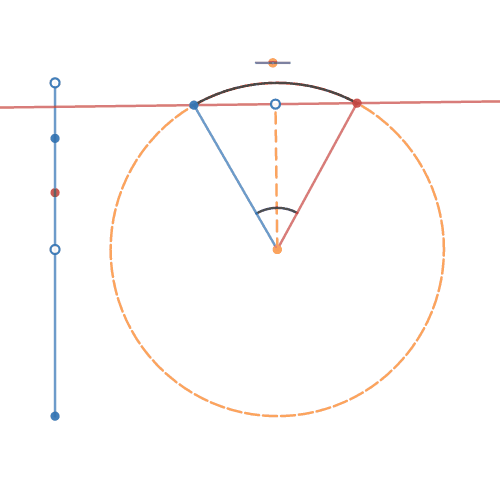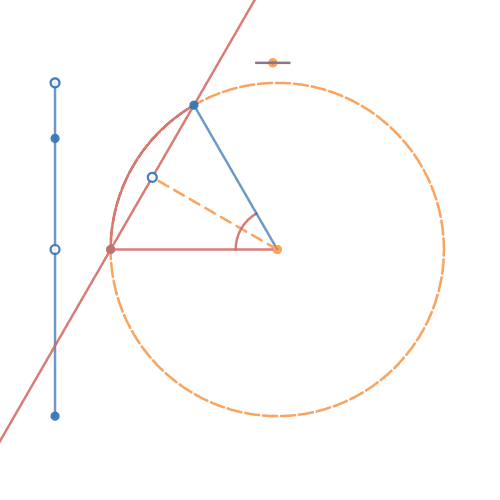
| Beregner skæringer mellem cirkler og linjer bestemt ved forskriften: a x + b y + c = 0, c = - ( a x₀ + b y₀ ) afledt af a ( x - x₀ ) + b ( y - y₀ ) = 0 ⇔ a x + b y - ( a x₀ + b y₀ ) = 0. Bemærk: For y = A x + B er 1) a = A og b = -1 2) x₀ = 0 og y₀ = B FriViden, video 33: Skæring ml. linie og cirkel Webmatematik: Cirkler og linjers skæringer |
lørdag den 30. januar 2016
Cirkel-linje-skæring 6
Cirkel-linje-skæring 5
| Beregner opgaver af typen: En cirkel har centrum i punktet ( -0,25 ; -0,3 ) og radius = 7,5. - Den skæres af en linje, som går gennem den 119. og 17. grad. Bestem skæringskoordinaterne. FriViden, video 33: Skæring ml. linie og cirkel Web-matematik: Cirkler og linjers skæringer Med fuldt skalerbare skydere og grafer! |
torsdag den 28. januar 2016
Parametrisk cirkel (scalable)
| FriViden (video 30): Cirklens ligning Webmatematik: Cirklens ligning Med fuldt skalerbare skydere og grafer! |
onsdag den 27. januar 2016
lørdag den 23. januar 2016
Vektorer (differens mellem vektorer)
| FriViden (video 3): Regning med vektorer i planen Webmatematik (Vektorer i 2 D): Regning med vektorer Forklaring Hvis -a→ angiver pilen fra B til A og c→ angiver pilen A til C, angiver differensen ( c→ - a→ ) = ( -a→ + c→ ) pilen fra B til C. Dermed er blå + grøn = rød: ( -a→ + c→ ) = b→ |
fredag den 22. januar 2016
torsdag den 21. januar 2016
Vektorer (vektortyper)
| FriViden (video 1): Introduktion til vektorer i planen Web-matematik: Vektorer Lod- og vandrette vektorer Ens- og modsatrettede vektorer Sted- og tværvektor Vektor mellem to punkter Enhedsvektor |
tirsdag den 19. januar 2016
mandag den 18. januar 2016
Skæring ( ligning / parameterfremstilling )
| Skæringspunktet mellem to linjer findes lettest ved at indsætte den ene linjes parameterfremstilling i den anden linjes ligning. FriViden (video 26): Skæring mellem linjer Webmatematik: Linjens parameterfremstilling |
søndag den 17. januar 2016
Vinkel mellem normalvektorer
| FriViden (video 23): Vinkler mellem linjer Webmatematik (vektorer): Vinkel mellem vektorer |
lørdag den 16. januar 2016
fredag den 15. januar 2016
Vektorer (linjens ligning)
| Ligger P ( x ; y ) på linjen, er P₀ ( x₀ ; y₀ ) = P, eller vektor ( P₀ P )→ ⊥ n→ ⇔ ( P₀ P )→ ⋅ n→ = 0 ⇔ ( x - x₀ ; y - y₀ ) ⋅ ( a ; b ) = 0 ⇔ a ⋅ ( x - x₀ ) + b ⋅ ( y - y₀ ) = 0 Fra normalvektor til ligning: ( x ; y ) = ( x₀ ; y₀ ) + t ( a ; b ) r→ = ( a ; b ) ⇔ n→ = ( -b ; a ) ⇔ -b ⋅ ( x - x₀ ) + a ⋅ ( y - y₀ ) = 0 ⇔ -b x + a y - ( a ⋅ y₀ - b ⋅ x₀ ) = 0 ⇔ -b x + a y + c = 0, c = -( a ⋅ y₀ - b ⋅ x₀ ). Fra ligning til parameterfremstilling: a x + b y + c = 0 n→ = ( a ; b ) ⇔ r→ = ( -b ; a ) x = 0: b y + c = 0 ⇔ y = -c / b ( x ; y ) = ( 0 ; -c / b ) + t ( -b ; a ) FriViden (video 21-22): Linjens ligning Webmatematik (vektorer): Linjens ligning Wikipedia: Line equation |
torsdag den 14. januar 2016
Vektorer (areal og vinkel)
| FriViden (Video 18): Arealberegning vha. determinant Webmatematik: Determinant Webmatematik: Vinkel mellem to vektorer Vinklen mellem to vektorer, der udgår fra samme punkt, kan bestemmes ved at tage cosinus invers til: produktet af deres x-koordinater + produktet af deres y-koordinater delt med: produktet af deres længder. |
Normal- og retningsvektor
| FriViden (video 17): Tværvektor Webmatematik: Vektorer To vektorer står vinkelret på hinanden (er ortogonale), hvis deres prikprodukt (det såkaldte skalarprodukt) er lig med nul: Det vil sige: hvis summen af 1. koordinaternes produkt og 2. koordinaternes produkt er lig med nul. Webmatematik: Skalarprodukt |
onsdag den 13. januar 2016
Linjens parameterfremstilling
 |
| ( 0 + 1t, b + at ) |
 |
| Parameterfremstillinger |
 |
FriViden (video 19 og 20):
Linjens parameterfremstilling
Webmatematik:
Linjens parameterfremstilling
Linjens ligning
Wikipedia:
Linear equation
Linjefremstilling
tirsdag den 12. januar 2016
mandag den 11. januar 2016
Vektorer (determinant)
| FriViden (video 15-16): Parallelle vektorer (determinant) Webmatematik: Determinant |
Vinkelbuer og -halveringslinjer
| Placer vinkel B og C til henholdsvis venstre og højre for vinkel A, og du har alle trekantens vinkler på den samme rette linje, hvilket viser, at trekantens vinkelsum er 180 grader. |
lørdag den 9. januar 2016
fredag den 8. januar 2016
Linjens ligning 1
| Lodret linje: x = k Vandret linje: y = k Skrå linje: y = a x + b y = a ( x - x₀ ) + y₀ y = a ( x - s ) + t Vandret forskydning: x₀ og s Lodret forskydning: y₀ og t |
lørdag den 2. januar 2016
Vektorer (punkt- og vinkelfinder)
FriViden: Video 6: Punktbestemmelse Video 6: Stedvektor Video 7: Ortogonale vektorer Video 9: Prikprodukt | Med vinkelberegning! der udgår fra samme punkt, kan bestemmes ved at tage cosinus invers til: produktet af deres x-koordinater + produktet af deres y-koordinater delt med: produktet af deres længder. Video 11: Vinkelbestemmelse Webmatematik: Vinkel ml. vektorer |
fredag den 1. januar 2016
Vektorer 4 (punktberegning)
FriViden: Video 6: Punktbestemmelse Video 11: Vinkelbestemmelse Web-matematik: Vinkel ml. vektorer | På linjen AB, der har koordinaterne A ( 2 ; -5 ) og B ( 14 ; 7 ), ligger punktet C, sådan at længden af vektor AC = 2 / 3 af AB. C's koordinatsæt bestemmes i det følgende: AB = ( 14 - 2 ; 7 - ( -5 ) ) = ( 12 ; 12 ) Stedvektoren OC, der (som forbogstavet O antyder) udgår fra origo, findes: OC = OA + AC = OA + ( 2 / 3 ) ⋅ AB = ( 2 ; -5 ) + ( 2 / 3 ) ⋅ ( 12 ; 12 ) = ( 2 ; -5 ) + ( 8 ; 8 ) = ( 10 ; 3 ) |
Abonner på:
Kommentarer (Atom)