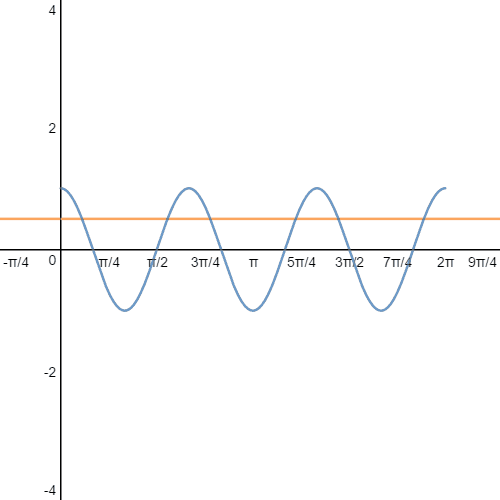
| g ( x ) = 12 f ( x ) = cos ( 3 ⋅ x ){ 0 < x < 2 ⋅ π } Perioden: p = 2 ⋅ π3 = 2,094 Vi løser ligningen f ( x ) = ½ 3 ⋅ x = cos−1 ( 12 ) x0 = cos−1 ( 12 )3 = 0,349 Dermed er: x1 = x0 + 1 ⋅ p = 2,443 x2 = x0 + 2 ⋅ p = 4,538 x3 = −x0 + 1 ⋅ p = 1,745 x4 = −x0 + 2 ⋅ p = 3,840 x5 = −x0 + 3 ⋅ p = 5,934 |

Ingen kommentarer:
Send en kommentar